Introduction to Marker Clustering With Google Maps
Heads up! This article was written in 2008. The theory itself is still good but the demos are currently broken.
Static Maps API has URL length limit of around 2048 characters. You can hit this limit quickly when adding lot of markers. You can keep URL short by clustering markers together.
Square Based Clustering
Clustering is usually done by dividing map to squares. Square size depends on map zoom level. Markers inside a square are then grouped into cluster. This technique has some limitations. Look at the following image.
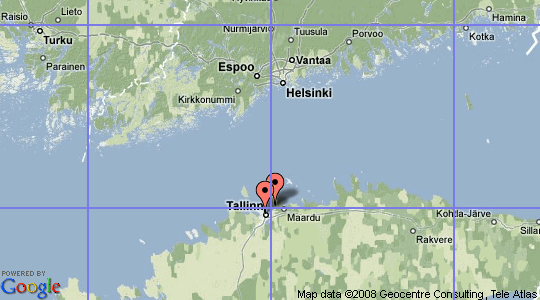
Two markers are close to each other. In fact they are so close they are overlapping. Both markers are also the only marker inside their square. Because markers are in separate square they wont be clustered.
Distance Based Clustering
We can also group markers together based on their distance from each other. We could cluster all markers inside 10 kilometer radius together. There is one problem with this approach. Kilometers (and miles) have different meaning in different zoom levels. In zoomed in map it might mean 100 pixels. In zoomed out maps one kilometer might be only one pixel.
There is only one distance unit which does not have this problem: pixels in current zoom level. One pixel on screen is always one pixel on screen. For example we want to cluster all markers which are 20 pixels from each other. I chose 20 pixels because it happens to be the distance after which markers start to overlap each other.
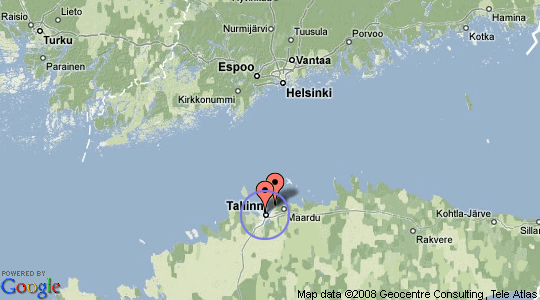
Now the two markers would be clustered since they are inside 20 pixel radius.
Distance Between Two Coordinates on Earth
Distance between two points on earth can be calculated in several ways. Haversine formula is reasonably accurate and widely used. It assumes earth is spherical (in reality earth is slightly ellipsoid). This causes accuracy to be +-2 km when calculating distances of around 20.000 km. 6371.0 km is used as average radius of earth.
Below is PHP implementation of Haversine formula:
function haversineDistance($lat1, $lon1, $lat2, $lon2) {
$latd = deg2rad($lat2 - $lat1);
$lond = deg2rad($lon2 - $lon1);
$a = sin($latd / 2) * sin($latd / 2) +
cos(deg2rad($lat1)) * cos(deg2rad($lat2)) *
sin($lond / 2) * sin($lond / 2);
$c = 2 * atan2(sqrt($a), sqrt(1 - $a));
return 6371.0 * $c;
}
But didn’t wee need distance in pixels instead? For that we can use Pythagoras' theorem. Pythagoras’ theorem uses cartesian (pixel) coordinates. Some Mercator magic can be used to convert latitude and longitude to pixel x and y values.
You might wonder where did number 268435456 come from? It is half of the earth circumference in pixels at zoom level 21. You can visualize it by thinking of full map. Full map size is 536870912 x 536870912 pixels. Center of the map in pixel coordinates is 268435456,268435456 which in latitude and longitude would be 0,0.
define('OFFSET', 268435456);
define('RADIUS', 85445659.4471); /* $offset / pi() */
function lonToX($lon) {
return round(OFFSET + RADIUS * $lon * pi() / 180);
}
function latToY($lat) {
return round(OFFSET - RADIUS *
log((1 + sin($lat * pi() / 180)) /
(1 - sin($lat * pi() / 180))) / 2);
}
function pixelDistance($lat1, $lon1, $lat2, $lon2, $zoom) {
$x1 = lonToX($lon1);
$y1 = latToY($lat1);
$x2 = lonToX($lon2);
$y2 = latToY($lat2);
return sqrt(pow(($x1-$x2),2) + pow(($y1-$y2),2)) >> (21 - $zoom);
}
Now we have all needed mathematics in place. What to do with them?
Cluster Markers Together
Let’s write example clusterer function. It takes three parameters:
- Array of lat and lon locations.
- Distance in pixel inside which markers will be clustered.
- Current map zoom level.
Function will return another array where coordinates closer than $distance are clustered together.
function cluster($markers, $distance, $zoom) {
$clustered = array();
/* Loop until all markers have been compared. */
while (count($markers)) {
$marker = array_pop($markers);
$cluster = array();
/* Compare against all markers which are left. */
foreach ($markers as $key => $target) {
$pixels = pixelDistance($marker['lat'], $marker['lon'],
$target['lat'], $target['lon'],
$zoom);
/* If two markers are closer than given distance remove */
/* target marker from array and add it to cluster. */
if ($distance > $pixels) {
printf("Distance between %s,%s and %s,%s is %d pixels.\n",
$marker['lat'], $marker['lon'],
$target['lat'], $target['lon'],
$pixels);
unset($markers[$key]);
$cluster[] = $target;
}
}
/* If a marker has been added to cluster, add also the one */
/* we were comparing to and remove the original from array. */
if (count($cluster) > 0) {
$cluster[] = $marker;
$clustered[] = $cluster;
} else {
$clustered[] = $marker;
}
}
return $clustered;
}
We can now test clusterer function with array of coordinates.
$markers = array();
$markers[] = array('id' => 'marker_1',
'lat' => 59.441193, 'lon' => 24.729494);
$markers[] = array('id' => 'marker_2',
'lat' => 59.432365, 'lon' => 24.742992);
$markers[] = array('id' => 'marker_3',
'lat' => 59.431602, 'lon' => 24.757563);
$markers[] = array('id' => 'marker_4',
'lat' => 59.437843, 'lon' => 24.765759);
$markers[] = array('id' => 'marker_5',
'lat' => 59.439644, 'lon' => 24.779041);
$markers[] = array('id' => 'marker_6',
'lat' => 59.434776, 'lon' => 24.756681);
$clustered = cluster($markers, 20, 11);
print_r($clustered);
If you run the code you can see how marker_3, marker_4 and marker_6 are clustered together. This can better be visualized as map screenshot before and after clustering. Blue marker is a cluster.
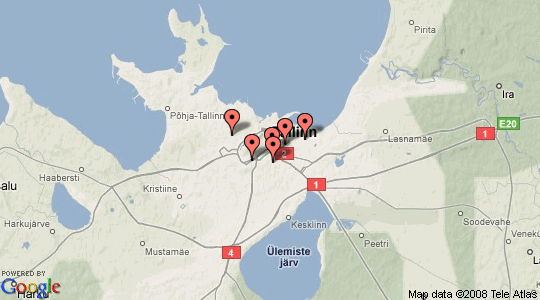
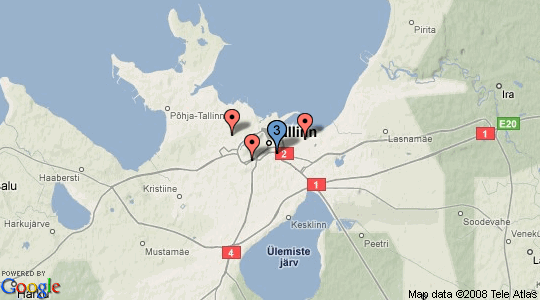
Real Life Usage?
Obviously making an array of coordinates into a new array of coordinates is not really usefull. However the first clusterer for Static Maps I committed to GitHub uses previously described technique. Clustering a static map takes only two extra lines of code. First create a cluster. Then add it to the map object. Rest is taken care automatically.
$clusterer = Google_Maps_Clusterer::create('distance');
$map->setClusterer($clusterer);
You can see it in action in capital cities of the world map. City locations are parsed from KML file. Note that in closer zooms locations are slightly off. Coordinates have only two decimals of latitude and longitude.
Currently I have demo code only for Static Maps. Serverside clustering for Google Maps API will follow soon. Thats a promise. Cross my heart.